«Учебник по дискретной математике. Сети, потоки в сетях. Теорема Форда – Фалкерсона»

Сетью называется связный граф (обычно, не орграф и не мультиграф), в котором заданы “пропускные способности” ребер, т. е. числа q_ij. Это числа большие или равные нулю, причем q_ij = 0 тогда и только тогда, когда нет ребра, соединяющего вершины i и j. Таким образом, можно считать, что пропускные способности ребер заданы для любой пары вершин. В дискретной математике пропускные способности ребер, как и все возникающие константы, считаются целыми числами (или рациональными, что одно и то же, так как рациональные числа отличаются от целых только единицами измерения). Заметим, что сети имеют огромные приложения, в частности, “сети планирования” (имеется в виду планирование производства некоторых новых, достаточно сложных изделий), где “пропускные способности” ребер – это время, за которое нужно из нескольких узлов изделия (вершин графа) получить другой (более сложный) узел. Сетевое планирование здесь не исследуется, так как гораздо больший интерес представляет сеть связи, где пропускные способности ребер – это обычно “количество одновременных разговоров”, которые могут происходить между телефонными узлами (вершинами графа).

Потоком в сети между вершиной t (источником) и s (стоком) называется набор чисел с_ij, (т. е. количество условного “груза”, перевозимого из вершины с номером i в вершину с номером j), удовлетворяющих четырем условиям:

1) числа с_ij Ј  0, причем если с_ij > 0, то с_ji = 0 (нет встречных перевозок);

2) числа c_ij Ј  q_ij (соответствующих пропускных способностей ребер);

3) если вершина с номером i – промежуточная (не совпадает с источником и стоком), то

,

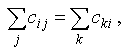
т. е. количество “груза”, вывозимого из вершины i, равно количеству “груза”, ввозимого в эту вершину;

4)  количество “груза”, вывозимого из источника t, должно быть равно количеству груза, ввозимого в сток s:

.

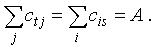
Число А называется величиной данного потока или просто потоком между t и s.

Для дальнейшего нам нужно следующее определение:

Пусть имеется некоторое сечение между вершинами t и s. Тогда величиной сечения называется сумма пропускных способностей ребер, входящих в это сечение. Сечение называется минимальным (максимальным), если его величина минимальна(максимальна).

Теорема Форда – Фалкерсона (1955). Максимальный поток между вершинами t и s равен величине минимального сечения между этими вершинами.

Доказательство этой теоремы является конструктивным (т. е. показывает, как найти нужный максимальный поток), поэтому приводится ниже.

1. Докажем сначала, что любой поток между вершинами t и s меньше или равен величине любого сечения. Пусть дан некоторый поток и некоторое сечение. Величина данного потока складывается из величин “грузов”, перевозимых по всем возможнымпутям из вершины t в s. Каждый такой путь обязан иметь общее ребро с данным сечением. Так как по каждому ребру сечения суммарно нельзя перевести “груза” больше, чем его пропускная способность, поэтому сумма всех грузов меньше или равна, сумме всех пропускных способностей ребер данного сечения. Утверждение доказано.

   Отсюда следует, что любой поток меньше или равен величине минимального сечения, а значит и максимальный поток меньше или равен величине минимального сечения.

2. Докажем теперь обратное неравенство. Пусть имеется некоторый поток c_ij (какой-то поток всегда существует, например, нулевой, когда все c_ij = 0). Будем помечать вершины графа, причем считаем, что все помеченные вершины образуют множество Y. Пометки вершин производятся от источника. Каждая пометка вершины (если эта вершина может быть помечена) состоит из двух чисел: первое – это “+” или “–” номер вершины (из Y), c которой связана новая помечаемая вершина, и второе – (обязательно должно быть положительным) – это фактически та добавка к потоку, которая может быть дополнительно “довезена” в эту вершину из источника по сравнению с исходным потоком.

Более точно, множество помеченных вершин Y образуется следующим образом:

источник t принадлежит Y и его пометка (0,Ґ ); второе число, условно говоря, равно бесконечности – что для дискретной математики означает, что это настолько большое число, как нам понадобится;

если вершина i принадлежит Y и c_ij < q_ij (дуга (i,j) – прямая и ненасыщенная), то вершина j также принадлежит Y и пометка вершины j равна (+i, d_j), где d_j>0 равно d_j= min {d_i, q_ij – c_ij}. Заметим, что здесь число d_i – это второе число уже помеченной вершины i,а знак + перед номером i означает, что дуга, связывающая вершины (i, j) является прямой (и ненасыщенной);

если вершина к принадлежит Y и с_jk > 0 (обратная дуга), то вершина с номером j также должна принадлежать Y и ее пометка равна (– к, d_j), где знак минус означает, что вершина j связана с уже помеченной вершиной к обратной дугой, d_j= min{d_k, q_jk+c_jk},причем очевидно, что d_j также строго больше нуля. Таким образом, построение множества Y является индуктивным, т. е. новая вершина добавляется в Y, если она связана с некоторой вершиной уже входящей в Y либо прямой ненасыщенной дугой, либо обратной дугой.

После того как построение множества Y закончено (к нему нельзя добавить новых вершин), возможны 2 случая.

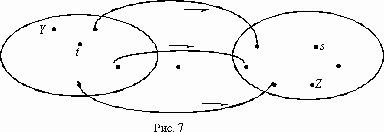
1. Сток (т. е. вершина с номером s) не входит в множество вершин Y. Тогда обозначим множество вершин, не входящих в Y через Z. Наш граф по условию является связным, поэтому из Y, в Z идут некоторые ребра. По правилам построения Y все эти ребра являются прямыми насыщенными дугами (рис. 7).

Ребра, идущие из множества Y в Z, образуют сечение между вершинами t и s. Видно также, что сумма пропускных способностей ребер этого сечения (а все эти ребра являются прямыми, насыщенными) равна потоку из t в s. Значит, данный поток является максимальным (так как он равен величине некоторого сечения), а данное сечение является минимальным.

2. Вершина s также входит в Y, и пусть второе число ее пометки d _s > 0. Тогда, очевидно, что между вершинами t и s существует цепь (состоящая из направленных ребер – прямых и обратных дуг), соединяющая эти вершины

Схематично это представлено на рис. 8.

t ® ·®·¬ ·¬·® ·®·¬ ·¬·®·®s

Рис. 8

Заметим, что дуга, выходящая из источника, и дуга, входящая в сток, должны быть обязательно прямыми. Прибавим d _s к c_ij для прямых дуг этой цепи (по построению видно, что полученное число будет меньше или равно q_ij) и вычтем это d _s из c_ij для обратных дуг (может получиться отрицательное число, но оно обязательно будет по абсолютной величине меньше q_ij, так как по построению d _s Ј  c_ij+q_ij , а это означает, что обратная дуга меняет направление, становится прямой дугой и его “нагрузка” будет равна модулю числа 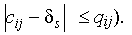Тогда новые числа для дуг, входящих в нашу цепь, а также “старые” c_ij для всех дуг, не входящих в нашу цепь, образуют новый поток из вершины t в вершину s (легко проверить простым рассуждением, что для новых чисел выполняются условия (1)–(4)). Кроме того, величина нового потока по сравнению со старым увеличилась на d_s > 0  . Для нового потока снова проведем ту же процедуру и т. д.

Так как каждый раз величина потока увеличивается, по крайней мере, на 1 (пропускные способности ребер являются целыми числами), а величина максимального потока ограничена (величиной минимального сечения), то эта процедура не может продолжаться бесконечно и, значит, на каком-то шаге получим поток, для которого вершина s не входит в Y, т. е. поток является максимальным и величина его равна величине минимального сечения. Теорема доказана.

Рассуждение теоремы Форда – Фалкерсона фактически является алгоритмом нахождения максимального потока между двумя вершинами (или доказательством того, что этот поток является максимальным). Подробный пример на эту тему приведен в разд. 15 “Решение типовых задач”.

Примечание. Если в данном графе с пропускными способностями ребер (т. е. сети) имеется несколько источников и несколько стоков, то описанный выше алгоритм можно применить следующим образом. Вводим новый источник и новый сток, причем новый источник соединяем ребрами со всеми источниками, а новый сток – со всеми стоками, при этом пропускные способности новых ребер считаем сколь угодно большими числами, так что эти дуги в любом возможном потоке были бы ненасыщенными (напомним, что ребра, идущие из источника и ребра, идущие в сток всегда являются прямыми дугами). После этого для нового графа решаем задачу о максимальном потоке (из одного нового источника в один новый сток). Решив ее, стираем все введенные ребра и вершины.

Рассмотрим еще некоторые вопросы (достаточно общего характера) из теории графов. Заметим, что в следующих разделах мы приводим только самые простые доказательства, а основные доказательства приведены в книге Р. Уилсона [6].