Поиск по сайту:
Смотри также:
Курсовой по дисциплине "Вычислительная математика" - Курсовая работа.
Современные этнодемографические процессы на территории Южно-Казахстанского экономического района - Курсовая работа.
Планирование карьеры в туризме - Курсовая работа.
Правовой статус осужденных - Курсовая работа.
Курсовая работа «Курсовая работа по математической логике и теории алгоритмов»
| Листов | 5 |
|---|---|
| Когда сдавалась работа | 2004 |
| Где сдавалась работа | БФ НГТУ |
| Оценка | Отлично (5) |
| Имя автора | Сергей |
Задание
1. Проверить двумя способами, будут ли эквивалентны следующие формулы: 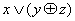 и
и 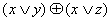 .
.
а) составлением таблиц истинности:
б) приведением формул к СДНФ или СКНФ с помощью эквивалентных преобразований:
2. С помощью эквивалентных преобразований приведите формулы к ДНФ, КНФ, СДНФ, СКНФ. Построить полином Жегалкина: 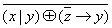 .
.
3. Найти сокращенную, все тупиковые и минимальные ДНФ булевой функции f(x, y, z) = f(0,0,1)=f(0,1,1)=f(1,0,0)=f(1,0,1)=1 двумя способами:
а) методом Квайна:
б) с помощью карт Карно:
Каким классам Поста принадлежит эта функция?
4. С помощью карт Карно найдите сокращенную, все тупиковые и минимальные ДНФ, КНФ булевой функции f(x1, x2, x3, x4), заданные вектором своих значений: (0111 1101 0010 1010).
5. Является ли полной система функций? Образует ли она базис?
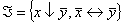 ;
;
6. Из данной совокупности секвенций выбрать доказуемые, построить их доказательства, для недоказуемых показать их недоказуемость с помощью: а) алгоритма Квайна, б) алгоритма редукции, в) метода резолюций.
а)┝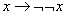
б) ┝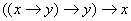
в) 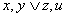 ┝
┝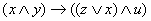
г) 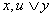 ┝
┝ 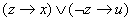
7. Привести к пренексной и клазуальной нормальной формам следующую формулу 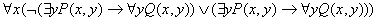 .
.
8. Методом резолюций проверить, противоречиво ли множество предложений 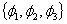 . Если множество непротиворечиво, то построить модель этого множества.
. Если множество непротиворечиво, то построить модель этого множества.
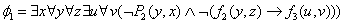
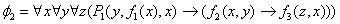
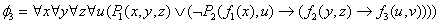
9. Доказать примитивную рекурсивность функций, выражая их через простейшие с помощью операторов суперпозиций и примитивной рекурсии

10. Построить машины Тьюринга для вычисления функций из задания 9.
f(x) = x-1;
