Поиск по сайту:
Смотри также:
Нотный редактор - Курсовая работа.
Оценка и анализ денежного потока на предприятии - Курсовая работа.
Управление качеством продукции на предприятии - Курсовая работа.
Ценные бумаги и деньги как объекты гражданского права - Курсовая работа.
Курсовая работа «Курсовой по дисциплине "Вычислительная математика"»
| Когда сдавалась работа | 2005 |
|---|---|
| Где сдавалась работа | БФ НГТУ |
| Имя автора | Сергей |
СОДЕРЖАНИЕ
Решить задачу методом бисекции: Две лестницы одна в 20 м длины, другая в 30 м, поставлены поперёк улицы и опираются своими концами на противоположные дома. Определить с точностью до 1 см ширину улицы, если точка пересечения лестниц находится на высоте 8 м над землей.
Решение: Рассмотрим треугольники ABC и AFG, они являются подобными (по двум сторонам и углу между ними). Следовательно, выполняются следующие соотношения:
Интегрирование. Вычислить интеграл по формулам трапеции и Симпсона с точность (1/2)*10-3: 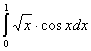 .
.
Вычисление интеграла по формуле трапеций.
Суть метода в следующем. Разобьём отрезок [a, b] на n равных частей длины h = (b-a)/n точками xi = a + ih (I = 0, 1, …, n), x0 = a, xn = b. Искомый интеграл равен сумме интегралов. На каждом элементарном отрезке [xi-1; xi] заменим подынтегральную функцию линейно функцией вида
y = A(x – xi-1) + B(x – xi), xÎ[xi-1; xi] (i=1,2,…,n).
Она в граничных точках xi-1, xi принимает те же значения, что и функция f(x). Её график является ломаной линией, начальная, угловые и конечная точки которой принадлежат также графику подынтегральной функции f(x). С увеличение n число общих точек будет расти, а в результате ломаная станет всё больше приближаться к кривой y=f(x).
Площадь трапеции можно вычислить по формуле:
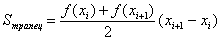 ;
;
Погрешность данного метода составляет:
Вычисление интеграла по формуле Симпсона.
Суть метода. Разобьем отрезок [a, b] на чётное число n = 2m равных частей длины h = (b-a)/(2m). Границы элементарных отрезков сузить x0 = a, x1, x2, …, x2m = b, так что x1 = x0+h, x2 = x1 + h = x0 + 2h, …, x2m = x2m-1 + h = x0 + 2mh. Кривую y = f(x) на отрезке [x2i-2; x2i] длины 2р аппроксимируем параболой
y = A(x – x2i-2)(x – x2i-1) + B(x – x2i-2)(x – x2i) + C(x – x2i-1)(x – x2i), (5)
таким образом, площадь под кривой приближённо заменим площадью под этой параболой.
Найдем коэффициенты A, B и C. Для этого в формуле (5) последовательно положим x = x2i = x2i-2 + 2h, x = x2i-1 = x2i-2 + h и x = x2i-2. Получим соответственно
Метод наименьших квадратов
Для функции cos(px) на отрезке [-1,1] найти среди многочленов третьей степени тот многочлен, который дает наилучшее приближение по методу наименьших квадратов, если использовать значения функции в точках:
x0 = -1; x1 = -0.5; x2 = 0; x3 = 0.5; x4 = 1.
Решить систему уравнений Ax=b методом Гаусса.
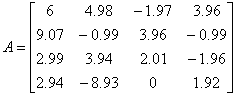
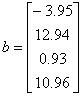
Применим простейший вариант метода Гаусса – схему единственного деления. Следуя Гауссу, сначала преобразуем квадратную матрицу коэффициентов при неизвестных к верхней треугольной матрице, из которой затем найдем решение системы.
Схема единственного деления состоит в следующем. Вначале исколючим неизвестное x1 из всех уравнений системы, кроме первого. Разделив первое уравнение на коэффициент а11 при x1. Далее, вычитая полученное уравнение, соответственное на a21, a31, a41 из (2) (3) и (4) уравнений, получим систему трех уравнений с тремя неизвестными.
На следующем шаге проделываем аналогичные преобразования. Исключив теперь x2. Объединяя полученные уравнения, придем к эквивалентной системе с треугольной матрицей коэффициентов.
Текст программы на MatLAB для решения данной системы уравнений:
Решение системы уравнений методом Зейделя:
Ax = b;
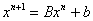
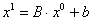 ,
, 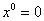 ;
;
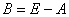 ;
;
Критерий окончания итераций:
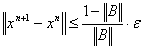 ;
;
e - заданная точность.
