Реферат «Преобразование скоростей в СТО»

Преобразования Лоренца

В 1895г., через год после ухода из жизни немецкого физика-экспериментатора Г.Герца, свет увидели преобразования координат Лоренца. Лоренц, в отличии от Герца, принадлежал к группе ученых, искавших альтернативное гипотезе увлечения решение проблемы Майкельсона. Справедливости ради отметим, что идея сокращения размеров ИМ вдоль оси X была высказана и Джорджем Фицджеральдом, но у Лоренца была конкретная теория, что и послужило причиной присвоения преобразованиям его фамилии.

Выражения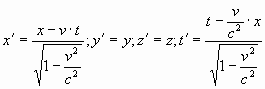 были получены Лоренцем, как преобразования координат и времени, оставляющие инвариантными вид уравнений Максвелла во всех инерциальных системах отсчета, при условии постоянства скорости распространения электромагнитного поля. Решаемая им задача может быть сформулирована следующим образом. Рассматриваются две системы отсчета. Первая считается покоящейся, вторая движущейся относительно первой с постоянной скоростью .

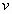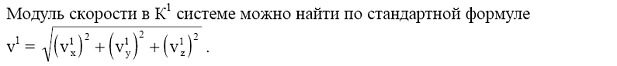
Следствия из преобразований Лоренца

1. Если в одной системе отсчета некоторые события происходят в точках x₁ и x₂ в один и тот же момент вр емени t, то в другой системе отсчета эти события происходят в точках x'₁ и x'₂ в разные моменты времени t'₁ и t'₂:

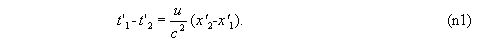
Понятие одновременности оказывается зависящим от выбора системы отсчета.

2. Если в одной системе отсчета между двумя событиями, происходящими в одной и той же точке, проходит время t, то в другой системе отсче та между этими же событиями проходит время

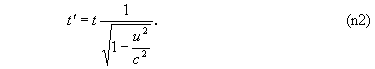
Это соотношение выражает релятивистский эффект замедления времени в движущихся объектах.

3. Если в одной системе отсчета покоящаяся линейка имеет длину l, то в системе отсчета, в которой линейка движется со скоростью u вдоль своей оси, ее длина

Этот эффект называется релятивистским сокращением продольных размеров тела. Поперечные размеры тела не изменяются при переходе в другие инерциа льные системы отсчета.

4. Если в одной системе отсчета тело имеет скорость v = (v_x, v_y, v_z), то его скорос ть v' = (v'_x, v'_y, v'_z) в другой системе отсчета равна

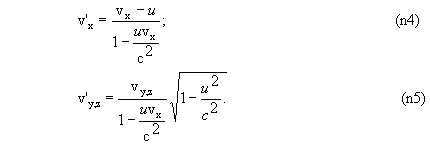
или в трехмерной векторной форме 
 

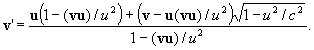
5. Из соотношени (n4), (n5) следует постоянство скорости c в различных системах отсчета. Действительно, если вычислить сумму квадратов левых частей этих равенств при условии

                         v²=(v_x)²+(v_y) ²+(v_z) ²=c²,                        (n6)

получим

                         v'²=(v'_x)²+ (v'_y)²+(v'_z) ²=c².                      (n7)

Т. е. скорость c одинакова по величине во всех инерциальных системах отсчета (независимо от направления). Заметим, что направления скоростей v и v' в общем случае различны в разных системах отсчета.

Закон сложения скоростей

Рассмотрим малое тело, движущееся в инерциальной системе отсчета k со скоростью u. Пространственно-временные координаты этого тела (t, r). Перейдем в другую инерциальную систему отсчета k' , начало координат которой движется относительно начала координат системы k со скоростью . Найдем скорость u' этого тела в системе k'.

Запишем преобразования для дифференциалов координат:

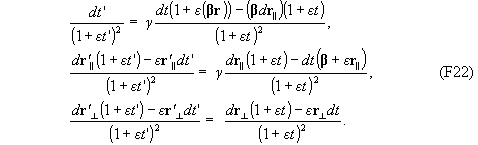
Введем вспомогательные величины r₀ = r-ut и r'₀ = r'-u't'. Разделим почленно второе и третье равенство (F22) на первое:

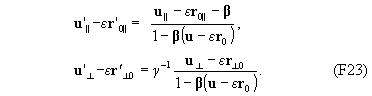
Полученные выражения связывают скорость тела, измеренную в системе k в пространственно-временной точке (t , r), со скоростью, измеренной в системе k' в той же точке с координатами (t', r'). Полученные выражения неудобны для практических расчетов, так как левые части равенств (F23) содержат скорость в неявном виде (через r'₀). Выразим координаты r'₀ через r₀ . Для этого запишем преобразования, подставив в левую часть координаты (t'=0, r'=r'₀):

С учетом первого равенства (F24) и определени r₀ =r-ut, получаем

Подставляя полученные выражения в правые части (F24), имеем

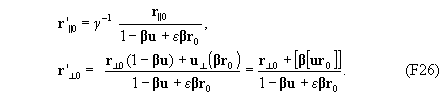
Теперь можно переписать равенства (F23)

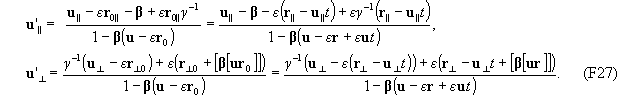
Несмотря на громоздкость, полученные соотношени удобны для непосредственных вычислений - подставляя в правые части равенств (F27) значения скорости тела в некоторой мировой точке (t, r) мы получаем скорость тела в произвольной инерциальной системе отсчета в той же мировой точке.

Список литературы:

1)      С. Н. Манида - Преобразования Лоренца-Фока: относительность бесконечности - Санкт-Петербургский госуниверситет

2)      Горохов А.В. - Элементы теории относительности

3)      http://www.sciteclibrary.ru