Поиск по сайту:
«Словарь по компьютерной и инженерной графике Э»
Файл: 4 КБ
Поделиться:
А Б В Г Д З И К Л М Н О П Р С Т У Ф Х Ц Ш Э
Эвольвента* (от лат. evolvens - разворачивающий) - кривая g?, для которой плоская кривая g является эволютой. Если r = r(s) (где s - натуральный параметр) - уравнение кривой g, то уравнение её эвольвенты имеет вид:
r = r(s) +t (c - s),
где с - произвольная постоянная, t - касательный вектор к g.
На рисунке показано построение эвольвенты в двух характерных случаях:
а) Для всех s
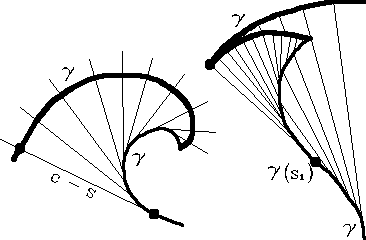
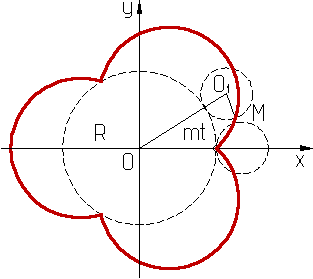
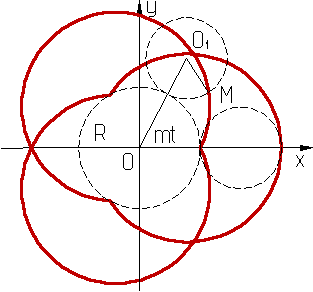
б) k(s) обращается в нуль при s = s1 причем k'(s1)#0 (точка эвольвенты, соответствующая s = s1, является точкой возврата 2-го рода).

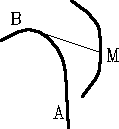
Эвольвента** [от лат. evolvens (evolventis) -разворачивающий] - развертка данной кривой АВ (см. рис.) - кривая, описываемая концом М гибкой нерастяжимой нити (закрепленной в некоторой точке), сматываемой с кривой АВ. Зубья многих зубчатых колес имеют эвольвентный профиль.

Элемент*- Обобщенный термин, под которым в зависимости от соответствующих условий может пониматься поверхность (часть поверхности, плоскость симметрии нескольких поверхностей), линия (профиль поверхности, линия пересечения двух поверхностей, ось поверхности или сечения), точка (точка пересечения линий, линии и поверхности, центр окружности или сферы).
Эллипс*(греч. elleipsis - недостаток) - линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающей все прямолинейные образующие одной полости этого конуса.
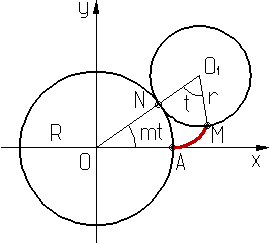
Эпициклоида* (от греч. epi - на, над, при, после и kukloz - окружность, круг) - плоская кривая, траектория точки производящей окружности радиуса r, катящейся без скольжения попо другой неподвижной окружности радиуса R, вне её (см. рис. 1, где 0 и 01 - центры неподвижной и производящей окружностей, N - точка их касания; М - вычерчивающая точка (А - её исходное положение), t - угол поворота производящей окружности, АМ - участок кривой).
Параметрические уравнения:
x = (R+mR) cos mt - mR cos (t+mt),
y = (R+mR) sin mt - mR sin (t+mt),
где m = r/R. Форма кривой зависит от значения m (на рис.2,а m=1/3, на рис. 2,б m =2/3). Если m =p/g (p и g - взаимно простые числа), точка М после g полных оборотов производящей окружности возвращается в исходное положение и эпициклоида - замкнутая кривая, состоящая из g ветвей с g точками возврата. Эпициклоида при m=1 - кардиоида. При m иррациональном число ветвей бесконечно, точка М в исходное положение не возвращается. Обобщением эпициклоид является эпитрохоида.

рис. 1.
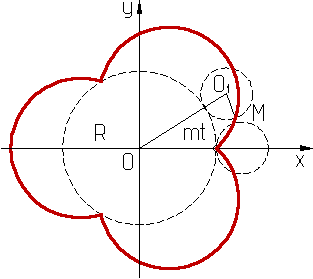
рис. 2.
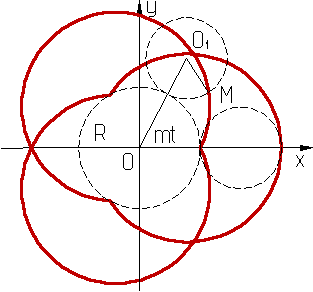
рис. 3
