«Словарь по компьютерной и инженерной графике Г»

габарит* (франц. gabarit) предельные внешние очертания предметов, сооружений и устройств. Габарит определяет возможность безопасного перемещения или правильного расположения какого-либо предмета среди других. На ж.-д. транспорте различают габарит подвижного состава и габарит приближения строений (зданий, сооружений, устройств) к ж.-д. путям. На автомобильных дорогах устанавливают габарит приближения конструкций мостов - предельные поперечные очертания, внутрь которых не должны заходить какие-либо элементы сооружения или расположенные на нем устройства. Подмостовой габарит - контур, базирующийся на судоходном горизонта; внутрь этого контура не должны заходить элементы пролетного строения и опор моста.

габарит** - предельные внешние очертания деталей, узлов, машин.

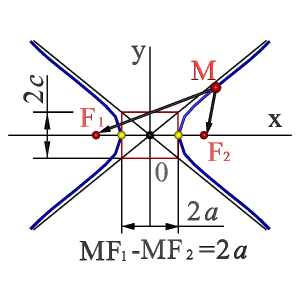
Гипербола* (греч. hyperbole) - плоская кривая линия;

- множество точек М плоскости разность (по абсолютной величине) расстояний F₁M и F₂M которых до двух определенных точек F₁ и F₂ этой плоскости (фокусов гиперболы) постоянна: F₁M - F₂M=2а<2с

Середина 0 отрезка F₁F₂ (фокусного расстояния) называется центром гиперболы *, **;

- линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающая обе его полости *, **;

- в прямоугольной системе координат 0ху с началом в центре гиперболы, на оси 0х которой лежат фокусы гиперболы уравнение гиперболы имеет так называемый канонический

х²/а² - у²/в²=1, в²=с² - а²,

где а и в длинны полуосей гиперболы *, **.

Гипоциклоида* (от греч. hupo - под, внизу и kukloeides -круговидный, круглый) - плоская кривая, траектория точки производящей окружности радиуса r, катящейся без скольжения по другой неподвижной окружности радиуса R внутри её (см. рис. 1, где 0 и 01 - центры неподвижной (радиуса R) и производящей (радиуса r) окружностей, N - точка их касания; М - вычерчивающая точка (А - её исходное положение), t - угол поворота производящей окружности, АМ - участок кривой

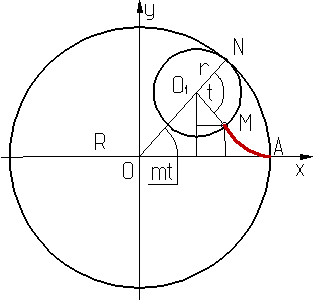
Рис. 1.

Параметрическое уравнение:

x = (R-mR) cos mt + mR cos (t-mt),

y = (R-mR) sin mt - mR sin (t-mt),

где m = r/R. Форма кривой зависит от значения m. Если m=p/g (p и g - взаимно простые числа), то M после g полных оборотов производящей окружности возвращается в исходное положение и гипоциклоида - замкнутая кривая, состоящая из g ветвей с g точками возврата при m<1/2 (рис. 2), при m>1/2 вместо g точек возврата имеет g угловых точек (рис.3).При m=1/2 гипоциклоида вырождается в диаметр неподвижной окружности, при m=1/4 является астроидой. При m иррациональном число ветвей бесконечно, точка М в исходное положение не возвращается. Обобщением гипоциклоиды является гипотрохоида.

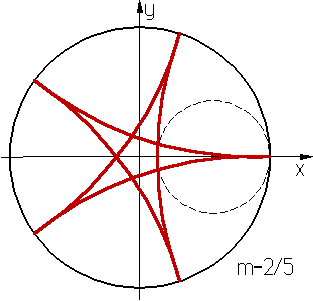
Рис. 2.

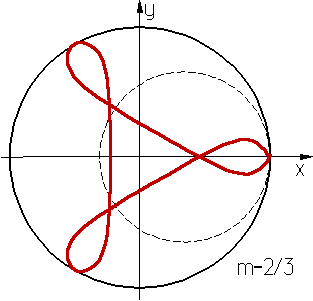
Рис. 3.